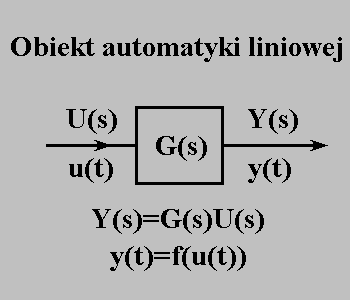
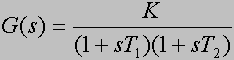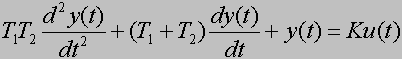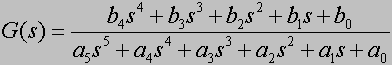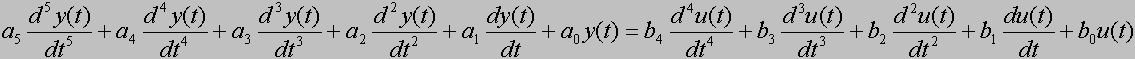Stanie się on bardziej podobny do równania opisującego obiekt proporcjonalny, jeśli przekształcimy go do postaci:
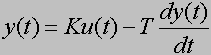
wtedy widać, że obiekt inercyjny to taki obiekt proporcjonalny, którego wyjście jest pomniejszone o szybkość zmian jakie się na tym wyjściu dokonują pomnożoną przez tzw. stałą czasową T. Ponieważ, jak widać, przez ową stała czasową mnożona
jest pochodna sygnału wyjściowego, więc odgrywa ona ważnę rolę w tym, jak szybko będą dokonywały się zmiany na wyjściu. Im mniejsza jest stała czasowa, tym bardziej obiekt inercyjny przypomina obiekt proporcjonalny, bo zmiany na wyjściu mogą dokonywać się szybciej.
Obiekt inercyjny ma bardzo ważna cechę: jeśli wymuszenie nie bedzie jakimś szczególnym sygnałem pochodzący z tzw. dziedziny dystrybucji, do której należy delta Diraca, to obiekt inercyjny zapewnia ciągłość sygnału na wyjściu. Tak więc jeśli nawet wymuszenie (wygnał wejściowy) będzie nieciągłe, to mimo to sygnał wyjściowy będzie ciągły i będzie się starał nadążać za wymuszeniem.
Przypuśćmy, że sygnały u(t) i y(t) miały do chwili to=0 wartości 0 (zero), zaś w chwili to=0 u(t)skoczył na wartość 1 (jeden) i utrzymywał już zawsze tą wartość. Sygnał taki zwie się skokiem jednostkowym. Obiekt proporcjonalny pomnożyłby tą nagłą zmianą wartości sygnału wejściowego. Obiekt inercyjny zachowa sygnał w chwili to, natomiast gwałtownie zmieni pochodną i to tak ją zmieni, żeby oczywiście spełnione było równanie:
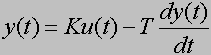
Ponieważ y(0)=0, u(0)=1, więc pochodna y'(0)=K/T.
Czyli widać, że obiekt inercyjny zachowuje ciągłość sygnału na wyjściu, ale nie zachowuje ciągłości pochodnej sygnału na wyjściu.
Pokuśmy się o małe usystematyzowanie: Obiekt proporcjonalny ze swej natury nie zachowuje ciągłości sygnału na wyjściu. Natomiast obiekt inercyjny jest obiektem pierwszego rzędu - zachowuje ciągłość sygnału na wyjściu, natomiast obiekt oscylacyjny, obiekt drugiego rzędu, o którym jest mowa poniżej - zachowuje ciągłość sygnału wyjściowego i ciągłość jego pochodnej.
Znaczenie stałej czasowej można zilustrować następującym przykładem: niech dwaj koledzy jeżdżą samochodami: jeden sportowym BMW, a drugi maluchem. Kiedy pierwszy "depnie" w swoim samochodzie na gaz, to samochód błyskawicznie przyśpiesza, a kierowca wciskany jest w fotel. Natomiast kierowca malucha może sobie "deptać", a i tak maluch rozpędzać się będzie powoli.
Ponieważ można uznać, że owe nagłe naciśnięcie na pedał gazu dokonane były w jednej chwili, więc można je przyrównać do skoku jednostkowego, natomiast prędkość samochodów - do sygnałów wyjściowych. BMW rozpędzało się błyskawicznie, a zatem w jego pośpiechu za wymuszeniem widzimy małą stałą czasową, no a maluch cóż - ma bardzo dużą stałą czasową.
Obiekt oscylacyjny
Transmitancja:
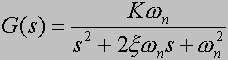
W dziedzinie czasowej obiekt oscylacyjny opisany jest równaniem:
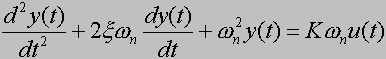
Parametr 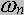 nazywany jest częstotliwością własną lub rezonansową, natomiast
nazywany jest częstotliwością własną lub rezonansową, natomiast 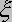 - tłumieniem. Jeśli
- tłumieniem. Jeśli 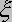 <1 to odpowiedź skokowa ma charakter oscylacyjny, w przeciwnym wypadku mówi się, że układ jest przetłumiony i wówczas w odpowiedzi na skok jednostkowy układ stopniowo dochodzi do wartości ustalonej.
Człon oscylacyjny może modelować różnego rodzaju układy drgające, do których należą zarówno układy mechaniczne, jak i elektryczne. Przykładami układów mechanicznych są różnego typu wahadła, a przykładem układów elektrycznych są tzw. układy rezonansowe.
Odpowiedź obiektu oscylacyjnego na skok jednostkowy przedstawia aplet na poniższym wykresie:
<1 to odpowiedź skokowa ma charakter oscylacyjny, w przeciwnym wypadku mówi się, że układ jest przetłumiony i wówczas w odpowiedzi na skok jednostkowy układ stopniowo dochodzi do wartości ustalonej.
Człon oscylacyjny może modelować różnego rodzaju układy drgające, do których należą zarówno układy mechaniczne, jak i elektryczne. Przykładami układów mechanicznych są różnego typu wahadła, a przykładem układów elektrycznych są tzw. układy rezonansowe.
Odpowiedź obiektu oscylacyjnego na skok jednostkowy przedstawia aplet na poniższym wykresie:
Mianownik transmitancji obiektu oscylacyjnego jest wielomianem zespolonym drugiego rzędu, a jak już wspominano - w dziedzinie liczb zespolonych wielomian stopnia n ma dokładnie n różnych rozwiązań, zatem zawsze mianownik można rozłożyć na czynniki liniowe, wówczas mianownik M(s) będzie miał postać:
M(s)=(s-s1)(s-s2)
Co więcej: wiadomo, że s2=s1*. Dzieje się tak dlatego, gdy 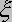 <1, a więc gdy wyróżnik jest mianownika transmitancji jest ujemny. Obwód fizyczny nanifestuje taką sytuację oscylacjami.
<1, a więc gdy wyróżnik jest mianownika transmitancji jest ujemny. Obwód fizyczny nanifestuje taką sytuację oscylacjami.
Gdy 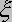 >1 wówczas mianownik transmitancji ma dwa pierwiastki rzeczywiste i transmitancja daje się wówczas wyrazić w postaci:
>1 wówczas mianownik transmitancji ma dwa pierwiastki rzeczywiste i transmitancja daje się wówczas wyrazić w postaci:
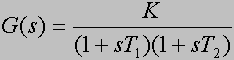
a równanie czasowe przybiera postać:
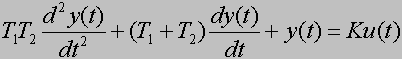
Na obiekt taki mówi się często: obiekt dwuinercyjny.
Gdy 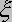 =1 wówczas wyróżnik mianownika jest zerem i wtedy T2=T1.
=1 wówczas wyróżnik mianownika jest zerem i wtedy T2=T1.
Obiekt piątego rzędu
Obiekt piątego rzędu został podany w postaci ogólnej, jako podsumowanie przeglądu podstawowych liniowych obiektów automatyki. Manewrując dpowiednio jego nastawami można uzyskać każdy obiekt niższego rzędu, w tym każdy obiekt, który został do tej pory na tej stronie przedstawiony.
<>BR>Aby Czytelnikowi ułatwić zadanie, tak jak we wszystkich wcześniejszych apletach w ostatnim oknie wyboru przygotowano gotowe przykłady, które są tak dobrane, aby wiernie odzwierciedlały przykłady z poprzednich apletów.
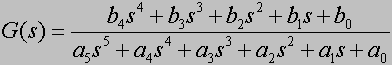
W dziedzinie czasowej obiekt piątego rzędu opisany jest równaniem:
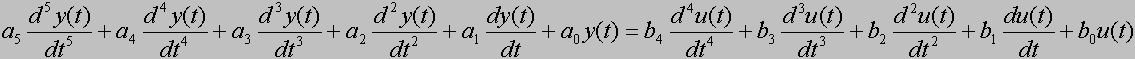
Odpowiedź obiektu piątego rzędu przedstawia aplet na poniższym wykresie, ale zanim zacznisz, Drogi Czytelniku, eksperymentować z apletem należy Cię przestrzec, że obiekt piątego rzędu jest o wiele trudniejszy do policzenia niż obiekty w poprzednich przykładach, dlatego musisz wykazać nieco więc cierpliwości, ponieważ obiekt ten liczy się wyczuwalnie dłużej:
Jak już wspomniano nie da się fizycznie zrealizować transmitancji w której w której stopień licznika jest większy niż stopień mianownika. Aplet zabezpiecza się przed podaniem niewłaściwych nastaw. Ściślej mówiąc zabezpieczenie to umieszczone jest w m-pliku, którego wykonanie daje odpowiedni wykres. M-plik jest wykonywany przez Matlaba. Matlab jest specjalizowanym programem do obliczeń numerycznych, ale nawet on "nie umie" obliczyć odpowiedzi dla obiektu, którego stopień licznika transmitancji jest większy od stopnia jej mianownika.
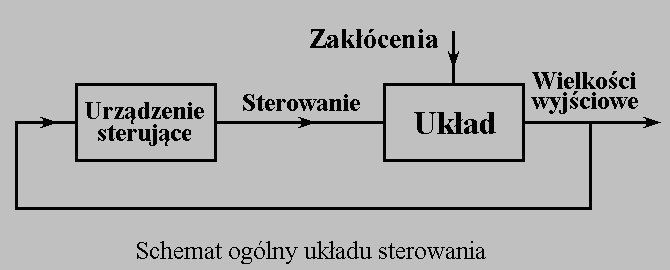
Podstawowe struktury układów sterowania
W przypadku kiedy chcemy oddziaływać na jednen, nieskomplikowany proces wtedy wykorzystuje się dwie proste struktury układów sterowania:
- układ otwarty,
- układ zamknięty zwany także układem regulacji,
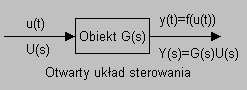
W otwartym układzie sterowania pobudza się wejście układu, lecz tego, co dzieje się na wyjściu układu nie wykorzystuje się w żaden sposób do określenia tego, w jaki sposób należy pobudzać wejście. Z takim rodzajem sterowania mieliśmy do czynienia w dotychczasowych apletach. Wadą takiego rozwiązania jest niewykorzystanie informacji o tym co dzieje się na wyjściu do określenia sposobu sterowania.
Sterowanie w układzie otwartym przypomina trochu sytuację błądzenia po omacku, zważywszy, że na wyjściu chcemy mieć określony stan, więc sterujemy, ale nie sprawdzamy, jaki jest ten stan. Wymaga to solidnej znajomości zachowania sterowanego obiektu i niezwykle precyzyjnego sterowania.
Ze sterowaniem w układzie otwartym mamy do czynienie podczas poszukiwania skarbu: idź trzydzieści kroków na północ od rozłożystego dębu, skręć na wschód, idź pięćdziesiąt kroków i kop. To jest sterowanie w układzie otwartym.
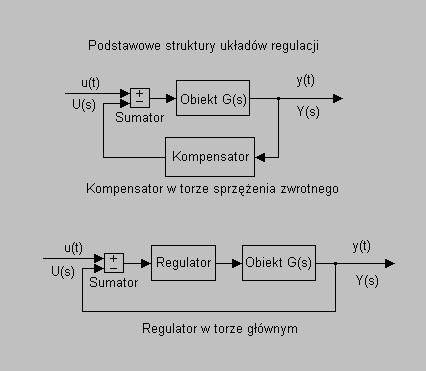
Zamknięte układy sterowania zwane są układami regulacji i wyróżnia się dwie podstawowe struktury, obie przedstawione na powyższym rysunku.
W zamkniętym układzie regulacji do określenia sposobu odziaływania na układ wykorzystywany jest stan wyjścia układu.
W układzie z kompensatorem w torze sprzężenia zwrotnego przetwarzany jest uchyb regulacji, czyli różnica pomiędzy sygnałem wejściowym a sygnałem wyjściowym, natomiast w układzie z regulatorem w torze głównym przetwarzana jest wartość wyściowa sygnału.
Poniższe aplety symulują układ regulacji z regulatorem w torze głównym.
Aplety te zostały napisane tak, że regulatorem może być regulator P,PI lub PID, natomiast obiektem może być obiekt proporcjonalny, inercyjny lub oscylacyjny.
P/K: Regulator P, obiekt proporcjonalny:
P/Osc: Regulator P, obiekt oscylacyjny
PI/K: Regulator PI, obiekt proporcjonalny:
PI/In: Regulator PI, obiekt inercyjny:
PI/Osc: Regulator PI, obiekt oscylacyjny
PID/K: Regulator PID, obiekt proporcjonalny:
PID/In: Regulator PID, obiekt inercyjny:
PID/Osc: Regulator PID, obiekt oscylacyjny:
Strona wciaz w rozbudowie.
cofnij sie
![]()
![]()
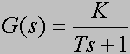
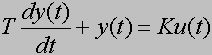
![]()
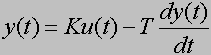
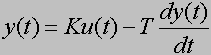
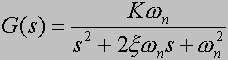
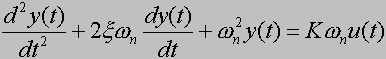
![]() <1, a więc gdy wyróżnik jest mianownika transmitancji jest ujemny. Obwód fizyczny nanifestuje taką sytuację oscylacjami.
<1, a więc gdy wyróżnik jest mianownika transmitancji jest ujemny. Obwód fizyczny nanifestuje taką sytuację oscylacjami.