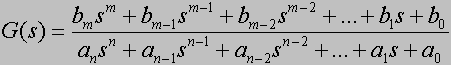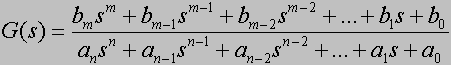Katedra Automatyki Napędu i Urządzeń Przemysłowych
Wydziału Elektrotechniki, Automatyki, Informatyki i Elektroniki
Akademii Górniczo-Hutniczej w Krakowie
Transmitancja
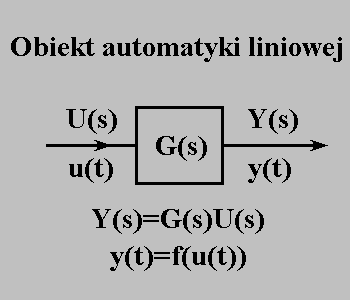
Samo pojęcie transmitancji jest dosyć proste, ale powtórzmy jeszcze raz:
- u(t) to sygnał wejściowy,
- y(t) to sygnał wyjściowy,
- G(s) to obiekt reprezentowany za pomocą tzw. transmitancji.
Na rysunku oprócz funkcji czasu u(t) i y(t) zaznaczono funkcje - sądząc z zapisu - U(s) i Y(s). Napis u(t) umieszczono obok strzałki symbolizującej sygnał wejściowy, napis y(t) obok strzałki symbolizującej sygnał wyjściowy, ale i napisy U(s) i Y(s) umieszczono obok tych strzałek. Dwa różne opisy tkwią przy tej samej wielkości: u(t) i U(s) przy sygnale wejściowym, y(t) i Y(s) przy sygnale wejściowym. Miałyby więc funkcje U(s) i Y(s) być jakimiś innymi postaciami funkcji u(t) i y(t)? Jeśli ktoś zadaje sobie takie pytanie, to z pewności zadaje sobie i drugie pytanie - po co? Po co, skoro u(t) i y(t) są funkcjami czasu, czyli - wydawałoby sie - bardzo dobrymi funkcjami? W dodatku U(s) i Y(s) są fukcjami jakiejś dziwnej zmiennej 's'. Co to za zmienna? Po co komu do szczęścia potrzebne jeszcze dziwaczne funkcje U(s) i Y(s)? Jak "powstają" U(s) i Y(s) z u(t) i y(t)?
Dziw nad dziwy, ale funkcje czasu wcale nie są dobrymi funkcjami. Albo raczej należałoby powiedzieć - nie są funkcjami wygodnymi w obliczeniach.
Aby uprościć sobie rachunki, zamieniane są na funkcje zespolone, a dokładniej U(s) i Y(s) są transformatami funkcji u(t) i y(t).
Ogólnie transmitancja, to stosunek sygnału wyściowego, do wejściowego.
Pozornie, niewiele można odnieść pożytku z takiej definicji.
Przykład transmitancji może być zaczepnięty z przypomnianego już wzoru U = R · i.
Oczywiście jest to tak prosty przykład, że niemalże nieodpowiedni, bo w dziedzinie zespolonej równanie to przyjmuje postać: Y(s)=RU(s), a więc transmitancja wynosi G(s)=R. Z punktu widzenia automatyki idealny opornik jest obiektem proporcjonalnym, który opisany jest równaniem y(t)=Ku(t). Jak widać transmitancja obiektu proporcjonalnego wynosi G(s)=K.
Ogólnie transmitancję można zapisać wzorem:
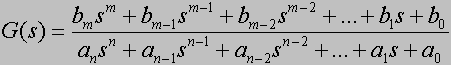
Chociaż transmitancja jest funkcją zmiennej zespolonej, to jej współczynniki an,an-1,an-2,...,a1,a0,bm,bm-1,bm-2,...,b1,b0 są najczęściej liczbami rzeczywistymi dodatnimi.
Nic nie jest warta dla automatyka transmitancja, która nie opisuje obiektu mogącego faktycznie istnieć. Jeśli tak jest, współczynnki te nazywane są często nastawami.
Przykłady transmitancji znajdzie Czytelnik przy omawianiu konkretnych obiektów. Tam też w apletach istnieje możliwość zmiany nastaw transmitancji i zobaczenia, jak się ten obiekt ze zmienionymi parametrami zachowuje.
Ponadto, podstawowym warunkiem aby transmitancja była realizowalna technicznie jest aby stopień mianownika nie był niższy niż stopień licznika, czyli aby n nie było mniejsze od m.
Zasadę tą ilustruje aplet, służący do zabawy nastawami obiektu piątego rzędu. Daje on możliwość zmiany jedenastu nastaw: a5,a4,a3,a2,a1,a0,b4,b3,b2,b1,b0 i nie pozwoli na wprowadzenie transmitancji niespełniającej powyższego warunku.