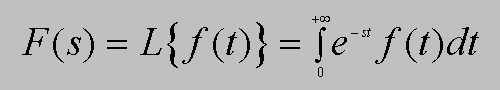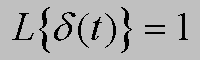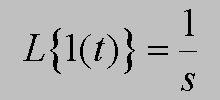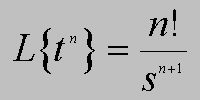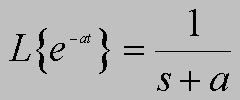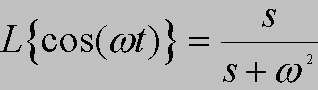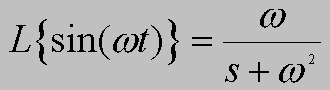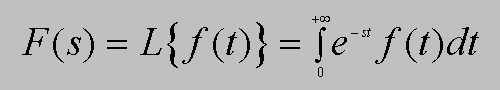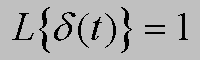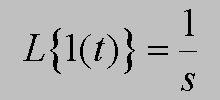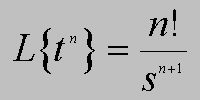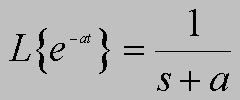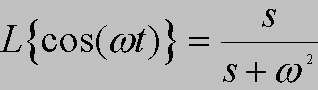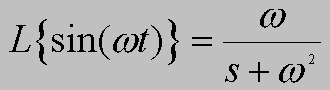Katedra Automatyki Napędu i Urządzeń Przemysłowych
Wydziału Elektrotechniki, Automatyki, Informatyki i Elektroniki
Akademii Górniczo-Hutniczej w Krakowie
Transformata Laplace'a
Transformata Laplace'a to nic innego jak maszynka to robienia innych funkcji: wrzucamy do niej wzór funkcji zmiennej rzeczywistej np. funkcji czasu, jak u(t) czy y(t), a w wyniku otrzymujemy funkcję zmiennej zespolonej 's'.
Transformata Laplace'a ma postać:
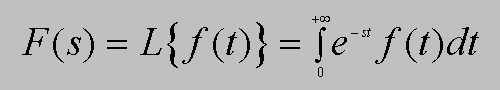
Funkcja f(t) nazywa się oryginałem (chyba ze zrozumiałeych powodów), natomiast funkcja zespolona F(s) uzyskana po przekształceniu oryginału - nazywa się transformatą.
Przyjrzyjmy sie teraz na kilku przykładach najbardziej typowych funkcji, jak działa to przekształcenie.
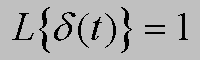
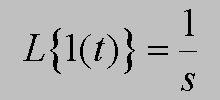
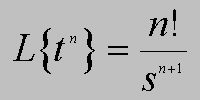
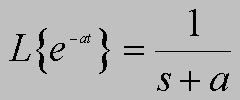
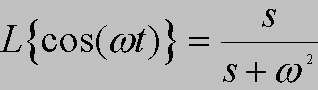
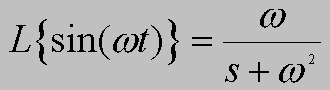
Chyba żadne przekształcenie nie "uczyniło" tyle dobrego, co transformata Laplace'a. Jeśli automatyk chce znać dynamiczne właśności obiektu, to pyta o jego transmitancję, która "wyrażona jest językiem" przekształcenia Laplace'a.
Funkcja potęgowa, ekspotencjalna, sinus i cosius, to rzeczywiście podstawowe funkcje, ale czym są tajemnicze funkcje 1(t) i d(t)?
Pierwsza to skok jednostkowy, a druga, to impuls Diraca. I tak, jak co dopiero zachwalano przekształcenie Laplace'a, tak tym razem nie sposób powstrzymać się przed pokusą stwierdzenia, że są to bodaj dwie najważniejsze funkcje w automatyce.
Przyjrzyjmy się ich wzorom:

Każdy kto zerknie na te wzory, z pewnością się zgodzi, że transformata jest o wiele prostsza niż oryginał