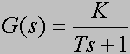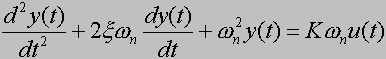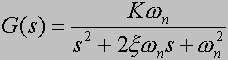gdzie s to liczba zespolona. Zbiór liczb zespolonych najczęściej oznacza się przez wielką literę C; napiszemy wówczas:

gdzie R jest zbiorem liczb rzeczywistych. Znak ![]() oznacza dodawanie, a znak
oznacza dodawanie, a znak ![]() oznacza mnożenie w zbiorze liczb zespolonych.
oznacza mnożenie w zbiorze liczb zespolonych.
![]()


j=(0,1)
![]()
a ponieważ liczbę zespoloną (-1,0) wolno nam utożsamić z -1, więc:
![]()
co zadaje kłam twierdzeniu, że każda liczba podniesiona do kwadratu jest nieujemna.
![]()

a skoro tak, to również definicje dodawania i mnożenia można zapisać w następujący sposób:

![]()
Gwiazdy nad sobą i gwiazdy pod sobą
I dwa obaczysz księżyce
pisał nasz wieszcz; owe odbite gwiazdy i księżyc też są sprzężone do tych prawdziwych.
![]()
![]()
Wykres tej funkcji można narysować na papierze, ponieważ jest nim zbiór punktów (x,x2) ale chyba nikt nie potrafi sobie wyobrazić (nie mówiąc o narysowaniu!) funkcji:
![]()
ponieważ już jej dziedzina jest dwuwymiarowa, dla zaznaczenia wartości potrzebne są kolejne dwa wymiary - w sumie wykres tej funkcji, to jakaś powieszchnia rozciągnięta w czerowymiarowej przestrzeni...
![]()
dlatego jego transmitancja wynosi:
![]()
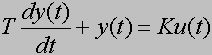
a transmitancja jego wynosi: