W obliczeniach wytrzymałościowych, oprócz prostych obciążeń, występują również złożone stany obciążeń, opisane przez przestrzenny układ naprężeń głównych ( s ₁ , s ₂ , s ₃ ). Dla prostych przypadków obciążeń obliczenia sprowadziły się do sprawdzenia warunku, aby naprężenia rzeczywiste obliczone z odpowiednich wzorów nie przekraczały wartości naprężeń dopuszczalnych. Dla złożonych przepadków obciążeń możemy postąpić w dwojaki sposób.
Po pierwsze odpowiednio zmieniany stosunek s ₁ : s ₂ : s ₃ naprężeń głownych, jaki istnieje w najbardziej zagrożonych punktach danego elementu mogłby dać odpowiedź na drodze doświadczalnej przez proporcjonalne zwiększanie naprężeń, aż do pojawienia się pierwszych pęknięć lub odkształceń plastycznych. Taka bezwzględna ocena stanu naprężeń jest pracochłonna i niepraktyczna i dlatego powstało wiele hipotez wytrzymałościowych stosujących ocenę porównawczą. Sposób ten polega na tym, że za porównawczy stan wytężenia (stopień zbliżenia się naprężeń do granicy Re, Rm, niebezpiecznej w określonym punkcie ciała) przyjmujemy najprostszy przypadek jakim jest jednoosiowe rozciąganie.

1. Hipoteza największych naprężeń normalnych ( s _max )

W myśl tej hipotezy, o wytężeniu materiału decyduje największe naprężenie normalne występujące w najbardziej zagrożonym punkcie ciała (rys.2.25).



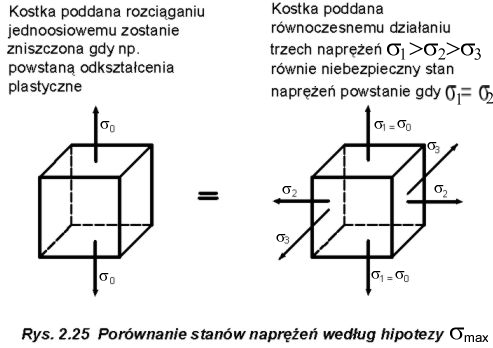
Naprężenia s ₂ i s ₃ nie mają wpływu na stan wytężenia materiału. Hipoteza ta ma znaczenie historyczne (może być stosowana dla materiałów kruchych: kamień, beton).

2. Hipoteza największych naprężeń tnących ( t _max)

Zgodnie z tą hipotezą, o wytężeniu materiału podczas zwykłej próby rozciągania nie decyduje osiągnięcie przez naprężenia rozciągające granicy plastyczności, lecz osiągnięcie przez naprężenia styczne wartości krytycznej.



W przypadku zwykłego rozciągania (por.2.8) naprężenia styczne wynoszą



zaś w trójkierunkowym stanie naprężeń



Porównując obie wartości naprężeń stycznych otrzymamy: s₀ = s₁ - s₃. Oznacza to, że naprężenie s ₁ może być większe od granicy (rys.2.26) plastyczności s _o , zanim powstanie w kostce krytyczny stan zapoczątkowujący płynięcie materiału.
Hipoteza ta jest stosowana dla materiałów plastycznych (stale niskowęglowe) i daje wyniki najbardziej zgodne z doświadczeniem.

 

3. Hipoteza Hubera

Naprężeniem zastępczym lub zredukowanym s₀ nazywamy naprężenie przy jednoosiowym rozciąganiu, równoważne wytężeniowo danemu stanowi naprężeń złożonych. Obliczenia wytrzymałościowe dla dowolnego przestrzennego stanu naprężeń sprowadzają się wówczas do sprawdzenia warunku (inaczej, warunku bezpieczeństwa):

(2.35)

Warunek ten, zgodnie z omówionymi hipotezami, będzie miał postać:

1. hipoteza s _max



(2.36)

2. hipoteza t _max



(2.37)

3. hipoteza Hubera

(2.38)

Jeżeli naprężenia w rozpatrywanym przekroju są wynikiem działania wielu rodzajów obciążeń, to:

• gdy naprężenia są tego samego rodzaju (wszystkie naprężenia normalne lub styczne), to naprężenie zastępcze jest sumą algebraiczną tych naprężeń,
• gdy naprężenia są różnego rodzaju, to naprężenie zastępcze wyznaczamy, korzystając z którejś hipotezy wytrzymałościowej.

Najczęściej spotykanym przypadkiem wytrzymałości złożonej jest pręt zginany momentem gnącym Mg oraz skręcany momentem skręcającym Ms.

Przykład 2.38.

Dla belki o przekroju kołowym zginanej momentem Mg i skręcanej momentem Ms wyznaczyć naprężenie zredukowane (zastępcze) według poznanych hipotez wytrzymałościowych.

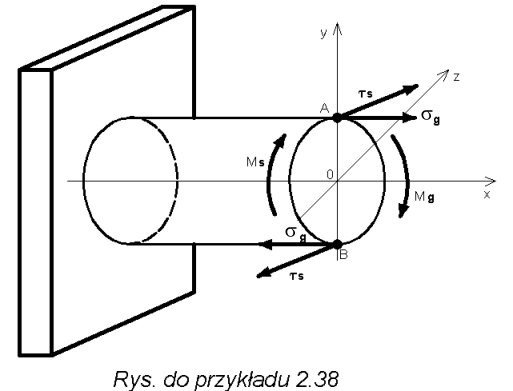
W przypadku pominięcia ścinania miejscami najbardziej wytężonymi będą punkty A i B. Stan naprężeń w tych punktach jest określony dwiema składowymi t _s , s _g .Zgodnie ze wzorem (2.12) mamy (musimy uszeregować s ₁ > s ₂ > s ₃ ):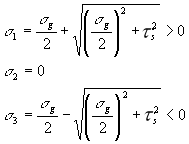

Stąd dla materiałów plastycznych (k_r = k_c) jak stale niskowęglowe, stopy metali nieżelaznych, otrzymamy:

a). według hipotezy t _max (por. 2.37)

b). według hipotezy Hubera (por. 2.38)

W przypadku zginania i skręcania wyrazimy powyższe wzory jako funkcje momentów Mg i Ms. Ponieważ dla przekroju kołowego i pierścieniowego wskaźniki zginania i skręcania są związane zależnościa W₀ = 2W_z , stąd podstawiając do powyższych wzorów:

oraz

otrzymamy wzory na moment zastępczy Mz:

a). według hipotezy t _max:

b). według hipotezy Hubera:

Naprężenia zredukowane s ₀ (inne oznaczenia s _red , s _z ) zgodznie ze wzorem 2.35 wyznaczymy z poniższego wzoru:

(2.39)

Przykład 2.39.

Płaskownik o przekroju prostokątnym (wykonany w dwóch wersjach: a) podcięcie niesymetryczne, b) podcięcie symetryczne) utwierdzony jednym końcem jest obciążony siłą P = 1,5 kN. Wyznaczyć naprężenia w przekrojach osłabionych podcięciem.

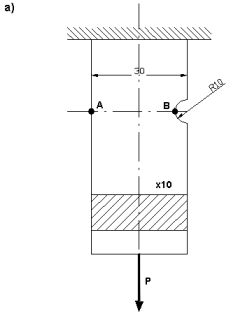
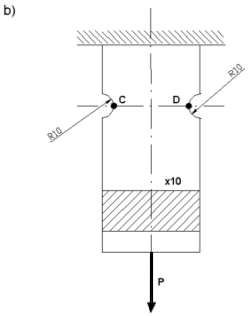
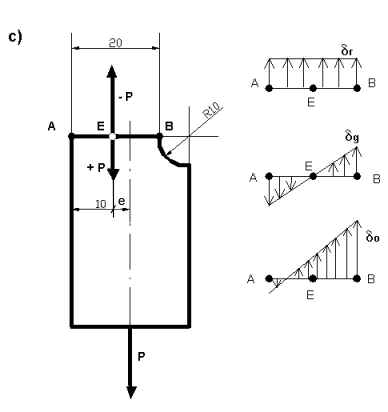
Rozwiazanie a)

W przekroju A-B przeprowadzamy redukcję sił zewnętrznych do środka ciężkości E (dwójka zerowa).

W przekroju tym wystąpią naprężenia rozciągające:

oraz naprężenia gnące (Mg = P× e)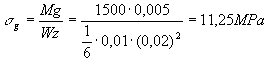

Naprężenia zredukowane s₀ w punkcie B wynoszą:

zaś w punkcie A odpowiednio:

Rozwiązanie b)

W przekroju C-D wystąpią tylko naprężenia rozciągające (środek ciężkości E leży na linii działania siły P ):

W wersji b (podcięcie symetryczne) naprężenia są mniejsze niż w wersji a (podcięcie niesymetryczne) mimo mniejszego pola przekroju w miejscu osłabionym.

 

Przykład 2.40.

Obliczyć średnicę belki w najbardziej niebezpiecznym przekroju, mając dane: obciążenie ciągłe q = 1000N/m², a = 1m, k_g = 100 MPa.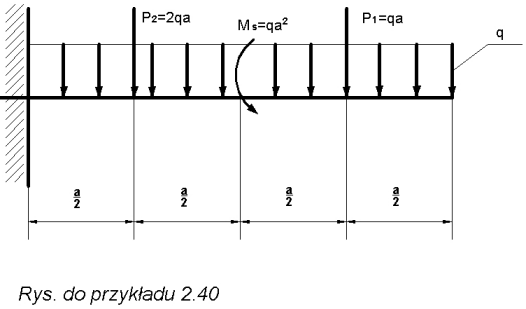

Odp. Średnica belki wynosi d = 7,8*10^-2 m.

Przykład 2.41.

Wyznaczyć naprężenia w miejscu utwierdzenia belki, mając dane Q = 40 kN, b = 36 mm, h = 100 mm, l = 100 mm, a = 30° .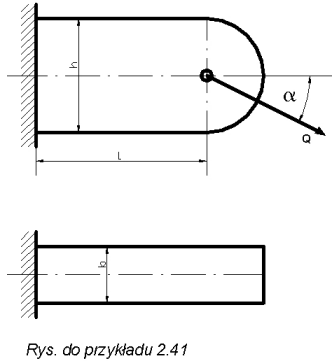

Odp. Naprężenia w miejscu utwierdzenia wynoszą s _z = 44 MPa.