2.3.5. Wyboczenie
2.3.5.1. Równanie linii ugięcia. Przykłady.
Przy omawianiu zagadnień rozciągania, ściskania, skręcania analizowaliśmy odkształcenia wywołane przez te rodzaje obciążeń. Odkształcenia jak wydłużenie, kąt skręcania, wykorzystano m.in. przy rozwiązywaniu zadań statycznie niewyznaczalnych. Ponieważ nie zajmujemy się zginaniem belek statycznie niewyznaczalnych, proble
m odkształceń belek zginanych wykorzystamy przy analizie wyboczenia.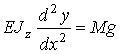
(2.30)
Po scałkowaniu równania (2.30) otrzymamy kąty q ugięcia osi pręta oraz równanie linii ugięcia (strzałkę ugięcia).
Przykład 2.37.
Dla belki obciążonej jak na rysunku wyznaczyć linię ugięcia oraz kąt ugięcia pręta.

Wyznaczamy reakcje podpór:
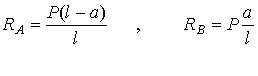
Wyznaczamy momenty gnące w poszczególnych przedziałach:
![]()
![]()
Równania różniczkowe linii ugięcia belki mają postać:
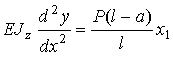
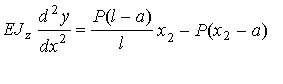
Po scałkowaniu otrzymamy kąty ugięcia:


Po ponownym scałkowaniu otrzymamy linię ugięcia:
![]()
![]()
Stałe całkowania C
1 , C2 , D1 , D2 wyznaczamy z warunków brzegowych oraz z warunków ciągłości:![]()
Po wyznaczeniu stałych całkowania otrzymamy kąty ugięcia osi belki na podporach.
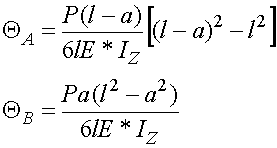
Strzałka ugięcia belki w połowie rozpiętości wynosi:
![]()
Jeżeli siła P będzie przyłożona w środku belki otrzymamy:
![]()
![]()
Znaki minus we wzorach na strzałki i kąty ugięcia można pominąć, jeżeli nie budzą wątpliwości.
Wzory na strzałki ugięcia
| schemat | kąt ugięcia | strzałka ugięcia |
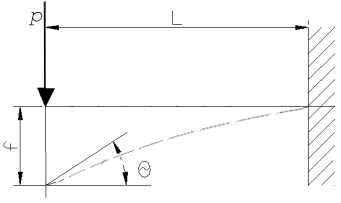 |
q = Pl2/2EJ | f = Pl3/3EJ |
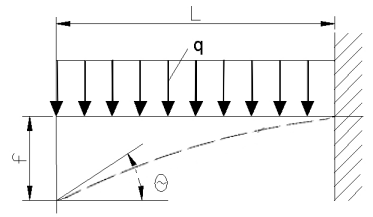 |
q = ql3/6EJ | f = ql4/8EJ |
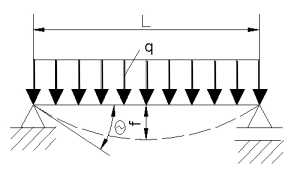 |
q = ql3/24EJ | f = (5/384)*(ql4/EJ) |
Tabela 2.3 - Wzory na odkształcenia belek zginanych
2.3.5.2.Wyboczenie pręta ściskanego
Ważnym zagadnieniem w wytrzymałości materiałów, oprócz obliczeń wytrzymałościowych, odkształcalności jest stateczność układu. Równowaga jest stateczna, jeżeli dowolnie niewielkie odkształcenie układu wywołuje siły przywracające mu postać pierwotną. Jeżeli siła ściskająca P pręt będzie wzrastać, to przy pewnej jej wartości P
kr minimalny impuls (Q = 0) (Rys.2.22a) spowoduje, że pręt nie wróci do prostoliniowego stanu równowagi lecz pozostanie w stanie równowagi przy krzywoliniowej postaci pręta.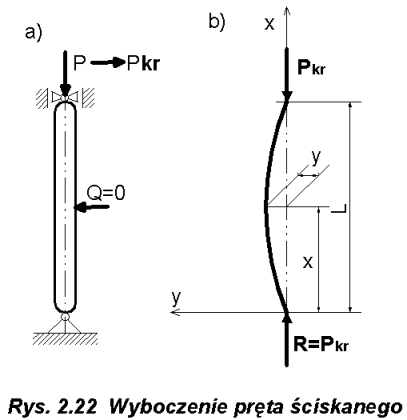
Jest to stan, gdzie oprócz ściskania siłą P
kr , powstaje również zginanie pręta momentem Mg = Pkr y, co może spowodować zniszczenie pręta nawet przy niewielkim wzroście siły ściskającej. Przejście układu ze stanu równowagi chwiejnej lub obojętnej (krzywoliniowa postać równowagi pręta) nazywamy utratą stateczności układu, a siłę powodującą zmianę stanu równowagi nazywamy siłą krytyczną Pkr (lub siłą wyboczającą). ![]()
(2.31)
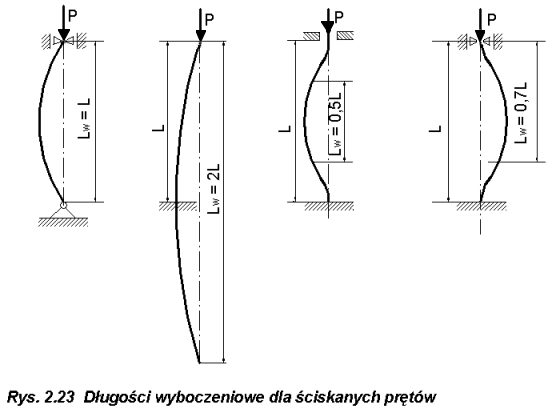
Jeżeli rozpatrzymy inne przypadki (rys.2.23) zamocowania końców pręta to otrzymamy wzory na siłę krytyczną, podobnie jak wzór (2.31). Zwróćmy uwagę, że przy innych mocowaniach pręta linie ugięcia składają się z fragmentów linii ugięcia podstawowego przypadku przedstawionego na rys.2.22
Wprowadzając pojęcie długości wyboczeniowej l
2.3.5.3.Naprężenia krytyczne. Granice stosowalności wzorów wyboczeniowych.
Jeżeli wyznaczymy siłę krytyczną, to oczywiście uzyskamy naprężenia krytyczne (s
kr = Pkr / F), przy których następuje utrata stateczności pręta ściskanego.![]()
a następnie wielkość charakteryzującą wymiary pręta:
![]()
zwaną smukłością pręta, otrzymamy wzór (2.32) na naprężenia krytyczne zwane wzorem Eulera:
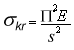
(2.32)
Wzór Eulera możemy przedstawić na wykresie we współrzędnych s, s
(Rys.2.24).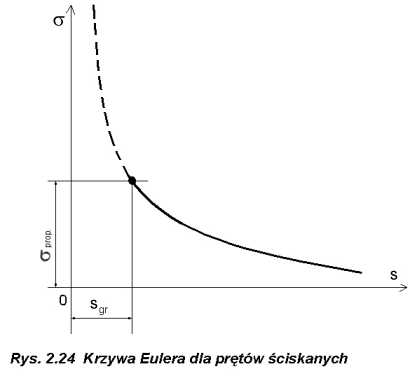
Ze wzoru (2.32) możemy korzystać tylko wtedy, gdy naprężenia nie przekraczają granicy stosowalności prawa Hook'a (s
kr Ł s prop), czyli: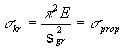 stąd
stąd 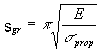
Obliczenia za pomocą wzoru (2.32) możemy przeprowadzić tylko wtedy, gdy smukłość pręta
s jest większa od smukłości granicznej Sgr. Dla smukłości mniejszej od Sgr stosuje się wzory (krzywe) otrzymane doświadczalnie dla danego materiału.2.3.5.4.Praktyczne metody przy obliczaniu prętów ściskanych.
W celu ominięcia kłopotów przy obliczaniu prętów ściskanych za pomocą wzoru Eulera i innych krzywych doświadczalnych skorzystajmy z normy PN-62/B-03200. Zgodnie z tą norma "Konstrukcje stalowe, obliczenia statyczne i projektowanie" sprawdzenie na wyboczenie pręta ściskanego siłą P przeprowadzamy według wzoru:
![]()
(2.33)
gdzie (b
< 1) jest współczynnikiem wyboczeniowym, zależnym od smukłości s pręta i granicy plastyczności Re materiału pręta (wg PN-62/B-03200).![]()
(2.34)
gdzie (m.w
> 1) jest współczynnikiem wyboczeniowym zależnym od smukłości s i wytrzymalości obliczeniowej R (wg PN-76/B-03200).