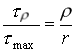
Skręcanie prętów o przekroju kołowym

2.3.4. Skręcanie prętów o przekroju kołowym

2.3.4.1. Podstawowe pojęcia przy skręcaniu

Skręcanie pręta (por. rys. 2.3) występuje wtedy, gdy dwie pary sił działają w dwóch różnych płaszczyznach prostopadłych do osi pręta.
Rozważmy pręt o przekroju kołowym i długości l (rys.2.20a) skręcany dwoma parami sił (momentami skręcającymi M_s)

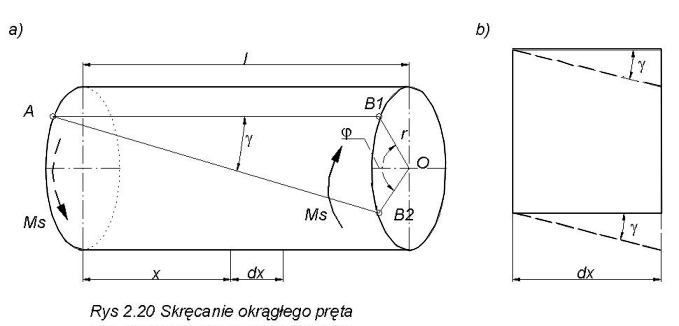
Prosta AB₁ równoległa do osi pręta na skutek skręcania przyjmie kształt linii śrubowej AB₂ o kącie g nachylenia jednakowym na całej długości pręta. Przekroje końcowe pręta pozostają nadal płaskie, zaś długość l i promień r nie ulega zmianie, czyli objętość pręta nie zmienia się. Jeżeli wyobrazimy sobie rozwinięty cylinder o szerokości dx, to widzimy (rys. 2.20b), że kąty proste odkształcą się o kąt g.
Ponieważ w pręcie nie zachodzą zmiany objętości, a jedynie zmiany postaci, można przyjąć, że stan naprężeń w pręcie skręcanym jest podobny do stanu czystego ścinania. W przekrojach poprzecznych pręta występują naprężenia styczne.

2.3.4.2. Analiza odkształceń i naprężeń w pręcie skręcanym

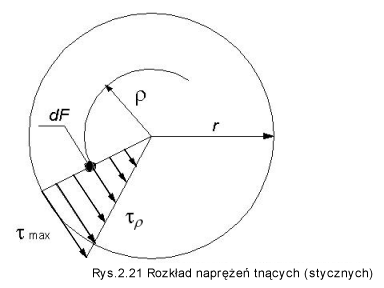
Naprężenia styczne w przekrojach poprzecznych, pręta są prostopadłe do pomyślanych promieni (rys. 2.21) i zmieniają się proporcjonalnie do zmian promienia (2.26) (potwierdzone wynikami badań).

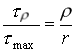
(2.26)

Z warunku równowagi rozpatrywanego pręta wynika, że suma elementarnych momentów ( dM=t_r*dF*r ) w przekroju poprzecznym pręta równa się momentowi skręcającemu (zewnętrznemu) dany pręt :

Otrzymamy w rezultacie:

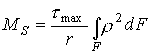
Występującą, tutaj całkę nazywamy J_o biegunowym momentem bezwładności przekroju (por. rozdz. 2.3.3.3)stąd wartość maksymalnych naprężeń statycznych t _max dla punktów położonych przy zewnętrznej powierzchni skręcanego pręta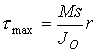

(2.27)

Kąt j ,o jaki obrócą się względem siebie końcowe przekroje poprzeczne pręta o średnicy d i długości l, wyraża się wzorem:

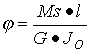
(2.28)

2.3.4.3. Obliczenia wytrzymałościowe. Przykłady.

Podobnie jak i przy zginaniu, wprowadzimy pojęcie wskaźnika wytrzymałości na skręcanie W_oJest to iloraz biegunowego momentu bezwładności J_o przez maksymalną odległość (skrajne włókna) od osi pręta:

Niektóre wzory na J_o oraz W₀ podano w tab. 2.2. Tak więc otrzymamy warunek wytrzymałościowy na skręcanie: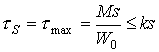

(2.29)

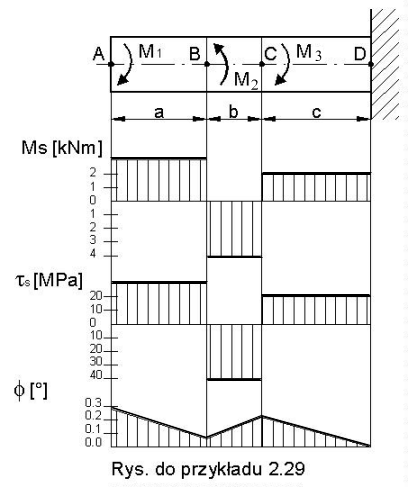
Przykład 2.29.

Okrągły pręt o średnicy F80 utwierdzony jednym końcem, obciążony jest trzema momentami jak na rysunku. Obliczyć i zrobić wykresy momentów skręcających naprężeń tnących oraz kątów skręcenia w poszczególnych odcinkach pręta.

a = 0,4 m
b = 0,2 m
c = 0,6 m

G = 8*10⁴ MPa
M₁ = 3 kNm
M₂ = 7 kNm
M₃ = 6 kNm

1. Obliczamy momenty skręcania w poszczególnych przedziałach:
M_S1 = M_AB = M₁ = 3kNm
M_S2 = M_BC = M₁ - M₂ = -4 kNm
M_S3 = M_CD = M₁ - M₂ + M₃ = 2 kNm

2. Obliczamy naprężenia styczne w poszczególnych przedziałach:
t_S1 = M_S1/W₀ @ 30 MPa
t_S2 = M_S2/W₀ @ -40 MPa
t_S3 = M_S3/W₀ @ 20 MPa

3. Obliczamy kąty skręcania w poszczgólnych przedziałach:
j_A = j_B + [(M_S1*a)/(G*I₀)] = 5*10^-3 rd
j_B = j_C - [(M_S2*b)/(G*I₀)] = 1,25*10^-3 rd
j_C = M_S3*c/G*I₀ = 3,73*10^-3 rd
j_D = 0rd

j^o = (180/P)j^(rd)
j_A = 0,286^o
j_B = 0,0715^o
j_C = 0,215^o
j_D = 0^o

Przykład 2.30.

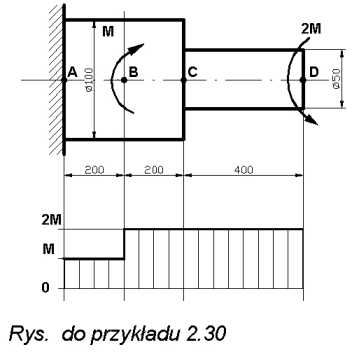
Obliczyć nośność wału przedstawionego na rysunku. Obliczyć także całkowity kat skręcenia wału.

G=8,5 10⁴MPa

ks=80 MPa

1. Wyznaczamy momenty w poszczególnych przedziałach: Ms₁ = M_BD = 2M ,Ms₂ = M_AB= 2M - M =M

2. Największe naprężenia wystąpią w części (CD)

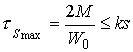
Stad wyznaczymy nośność (czyli maksymalny moment jakim można obciążyć wał) wału:

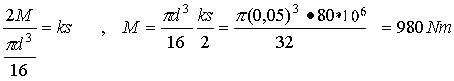
3. Całkowity kąt skręcenia wynosi:

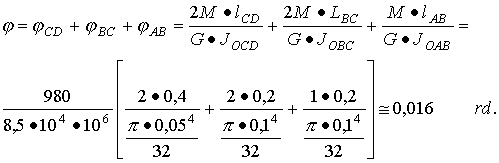
Przykład 2.31.

Dla wału obciążonego jak na rysunku zrobić wykres, momentów skręcających oraz wyznaczyć kąt obrotu swobodnego końca wału. Moduł odkształcenia postaciowego wynosi G.

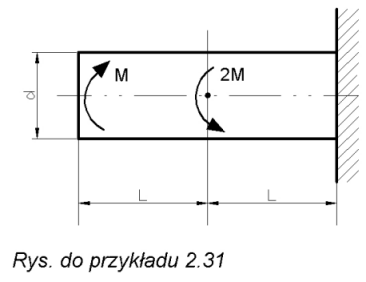
Odp. Kąt obrotu swobodnego końca wału: j = O.

Przykład 2.32.

DIa wału wydrążonego, obciążonego jak na rysunku wyznaczyć największe naprężenia tnące oraz obliczyć kąt, o jaki obróci się przekrój w punkcie A. Moduł odkształcenia postaciowego wynosi G=8,5*10⁴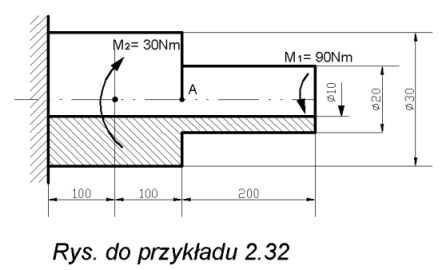 MPa .

Odp. Największe naprężenia tnące wynoszą t _s=61,2 MPa , zaś kąt skręcenia j _A=22,5 10^-4 rd .

2.3.4.4 Skręcanie wałów statycznie niewyznaczalnych. Przykłady.

Jest to problem, podobnie jak w rozdziale 2.3.1.4 nierozwiązywalny na gruncie statyki ciała doskonale sztywnego. Dodatkowe równania możemy otrzymać wykorzystując odkształcalność (kąt skręcenia) skręcanych prętów:

Przykład 2.33.

Dla belki o średnicy d, utwierdzonej obustronnie w nieodkształcalnych ścianach wyznaczyć reakcje utwierdzenia oraz wykonać wykres momentów skręcających.

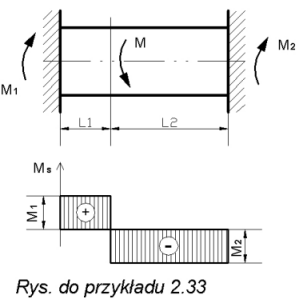
Oznaczmy reakcje utwierdzenia belki , momentami M₁,M₂,.Z warunku równowagi statycznej otrzymamy:

M₁-M+M₂=0

Z warunku sztywności (ciągłości albo zszycia) otrzymamy brakujące równanie. Kąt o jaki obróci się przekrój w miejscu obciążenia momentem M względem utwierdzonych końców jest jednakowy dla obu części belki.

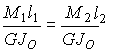
Stąd otrzymamy momenty utwierdzenia:

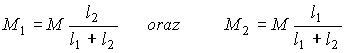
Wyznaczamy momenty skręcające w poszczególnych przedziałach:

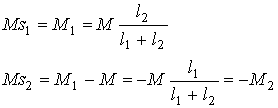
Przykład 2.34

Dla wału jak na rysunku wyznaczy momenty utwierdzenia.

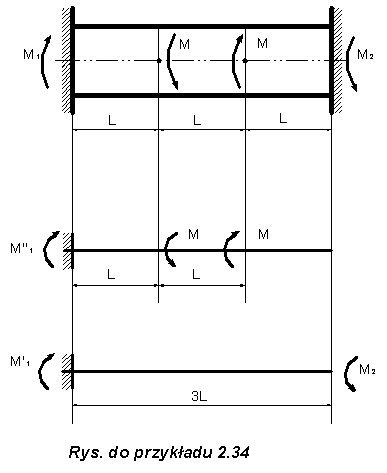
Z warunku równowagi otrzymamy:

M₁ - M + M - M₂ = O stąd M₁= M₂

Z warunku odkształceń wykorzystując zasadę superpozycji otrzymamy dodatkowe równanie.
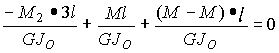
W miejscu utwierdzenia M₂ suma odkształceń (kątów skręcenia) wynosi zero

Momenty utwierdzenia wynoszą odpowiednio:

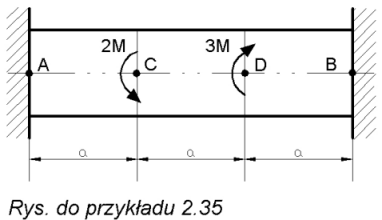
Przykład 2.35.

Dla pręta o przekroju kołowym obciążonym jak na rysunku wyznaczyć momenty utwierdzenia oraz największe naprężenia styczne.

Odp. Momenty utwierdzenia wynoszą

Przykład 2.36.

Rurę stalową połączono z prętem stalowym i zamocowano między dwiema sztywnymi ścianami. W miejscu połączenia układ obciążono momentem skręcającym M=6Nm Wyznaczyć wartość naprężeń w pręcie i w rurze oraz kąt skręcenia w miejscu połączenia.

Odp. Naprężenia w pręcie wynoszą t = 2,3 MPa, zaś w rurze t = 1,9 MPa, Kąt skręcenia ma wartość j =0,07°.