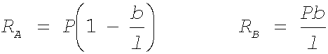
2.3.3. Zginanie
2.3.3.1. Podstawowe pojęcia przy zginaniu
W rozdziale 2.2.1 dowolny układ sił można było zredukować do jednej wypadkowej i do jednej pary sił.
Weźmy pod uwagę pręt, zaś w jego dowolnym przekroju poprzecznym za punkt redukcji przyjmijmy środek tego przekroju. Jeżeli w tym przekroju układ sił sprowadza się tylko do jednej składowej momentu zginającego Mg, to mamy do czynienia z czystym zginaniem (rys. 2.14a). Jeżeli występuje również siła styczna (tnąca) (rys. 2.14b), to mamy przypadek zginania z udziałem sił poprzecznych.
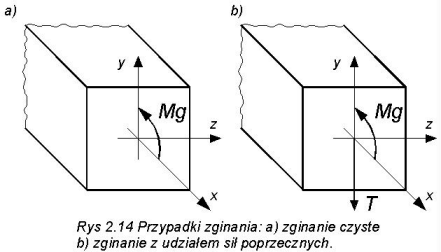
rys. 2.14
Jeżeli siły czynne (obciążenia zewnętrzne) i siły bierne (reakcje) działające na pręt zginany leżą w jednej płaszczyźnie, to płaszczyznę tę nazywamy płaszczyzną zginania.
Gdy płaszczyzna zginania pokrywa się z płaszczyzną główną zawierającą oś pręta (czyli zawierającą środki ciężkości przekrojów poprzecznych pręta), to przypadek taki nazywamy zginaniem prostym w odróżnieniu od zginania ukośnego (oś pręta staje się krzywą przestrzenną).
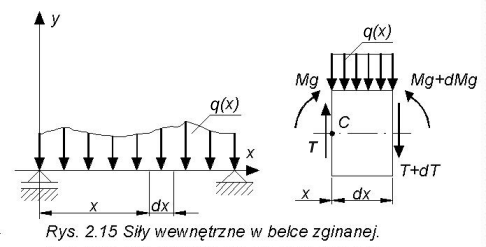
Wytnijmy w myśli z belki odcinek o długości
dx (o grubości jednostkowej). Po przeanalizowaniu warunków równowagi wyciętego odcinka otrzymamy związki między siłą tnącą, momentem gnącym i obciążeniem ciągłym: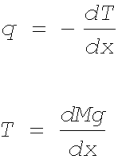
(2.19)
2.3.3.2. Wykresy sił tnących i momentów gnących
Do obliczeń wytrzymałościowych belek zginanych (przedstawionych w dalszych rozdziałach) potrzebne są wykresy sił tnących i momentów gnących.
Przykład 2.22.
Rozważmy belkę obciążoną siłą skupioną
P spoczywającą na dwóch podporach (przegub przesuwany i przegub nieprzesuwny).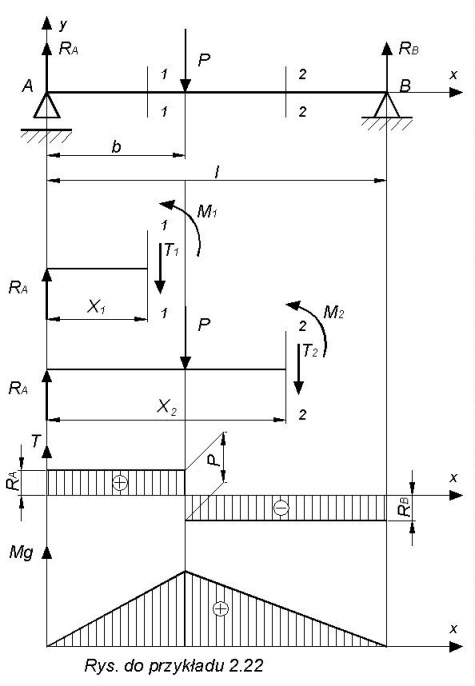
Wyznaczmy reakcje w podporach z warunków równowagi belki:
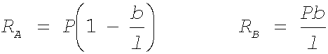
Rozpatrzmy przekrój poprzeczny (1-1). Oddziaływanie odrzuconej myślowo prawej części belki zastępujemy siłą tnącą
T1 i momentem gnącym M1. Z warunków równowagi rozpatrywanej części belki otrzymamy: 0 Ł x1 Ł b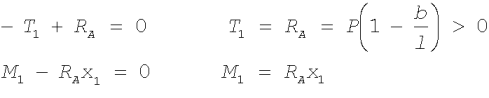
W przekroju poprzecznym (2-2) otrzymamy: b Ł x2 Ł l
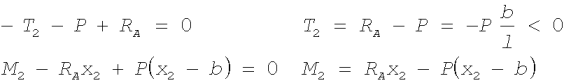
Wykorzystując wzory (2.19) otrzymamy również wyrażenia na
T1 i T2 (co może być wykorzystane do sprawdzenia poprawności obliczeń.Przykład 2.23.
Jako następny przykład rozpatrzmy belkę obciążoną siłą skupioną, momentem gnącym, obciążeniem ciągłym.
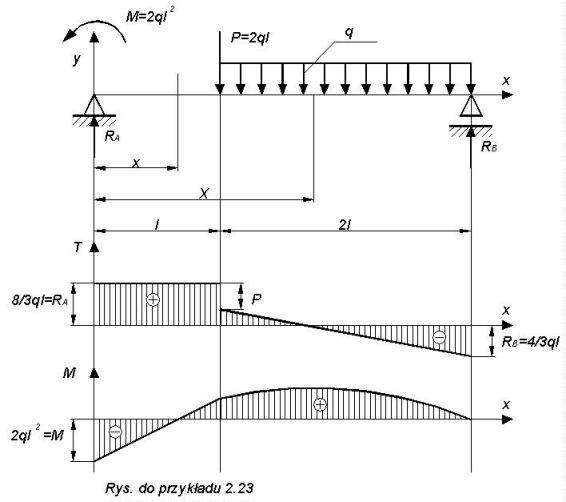
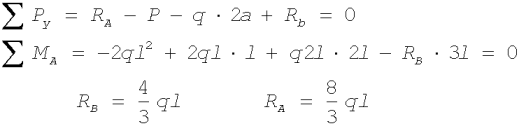

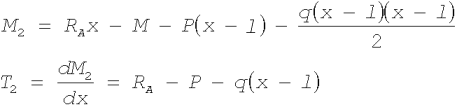
Wnioski praktyczne:
1)Na końcu belki (który nie jest obciążony momentem skupionym) moment zginający jest równy zeru.
2)Wartość bezwzględna siły tnącej na podporze jest liczbowo równa reakcji (składowej pionowej reakcji).
3)Wykres momentu zginającego ma skok wyłącznie w miejscu przyłożenia momentu skupionego. Wartość tego skoku jest równa wartości momentu skupionego.
4)Moment zginający w miejscu utwierdzenia równy jest, co do wartości bezwzględnej, momentowi reakcyjnemu utwierdzenia.
5)Wykres momentu zginającego ma załamania wyłącznie w miejscach działania sił skupionych, co na wykresie sił tnących uwidacznia się skokiem. Wartość tego skoku równa jest wartości siły skupionej.
6)Przy wyznaczaniu największych (bezwzględnych) wartości momentu zginającego należy wziąć pod uwagę: końcowe punkty belki (belki utwierdzone), punkty zerowania się siły tnącej, punkty przyłożenia sił skupionych.
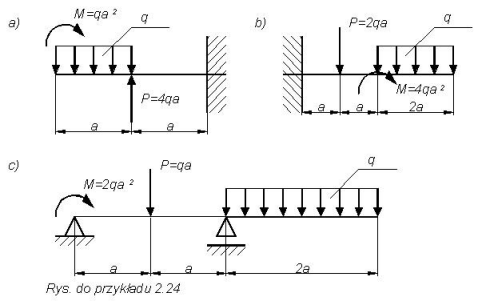
Przykład 2.24.
Sporządzić wykresy momentów zginających oraz sił tnących dla belek jak na rysunku.
2.3.3.3. Wprowadzenie do teorii momentów bezwładności figur płaskich
Naprężenie możemy przedstawić jako iloraz uogólnionej siły przez uogólniony przekrój. W przypadku rozciągania, ścinania będzie to siła rozciągająca, ścinająca i przekrój poprzeczny. W przypadku skręcania i zginania będzie to moment skręcający, zginający i wskaźnik przekroju na skręcanie czy zginanie, przy obliczaniu którego potrzebna jest znajomość momentów bezwładności przekroju.
Łatwo zauważymy, że przy zginaniu np. płaskownika przy jednakowym obciążeniu odkształcenie jego będzie zależeć od tego, w której płaszczyźnie działa moment zginający (rys. 2.16).
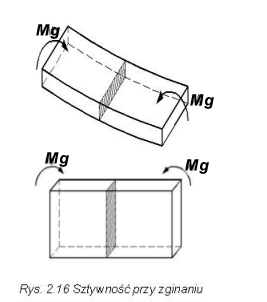
Wynika z tego wniosek, że odkształcenie elementu (sztywność) zależy nie tyle od wielkości pola przekroju, ile od rozmieszczenia tego pola wokół osi przy zginaniu.
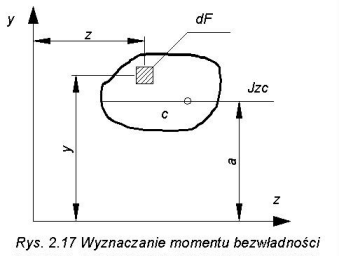
Momentem bezwładności
Jz figury płaskiej względem osi z nazywamy sumę iloczynów elementarnych pól dF tej figury i kwadratów odległości tych pól od osi z (rys. 2.17).![]()
(2.20)
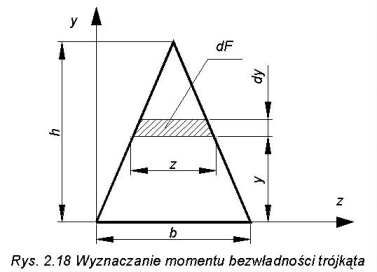
W przypadku trójkąta o podstawie b i wysokości h elementarne pole wynosi:
dF=z*dy=[b(h-y)/h]*dy
i moment bezwładności:
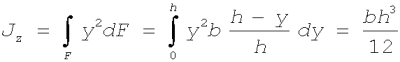
Przy wyznaczaniu momentu bezwładności Jz, można skorzystać ze wzoru Steinera.
![]()
(2.21)
Moment bezwładności
Jz względem osi jest równy sumie momentu bezwładności względem osi przechodzącej przez środek ciężkości Jzc oraz iloczynu pola figury F i kwadratu odległości między tymi osiami -a- (rys. 2.17). Ze wzoru (2.21) korzystamy przy obliczaniu momentów bezwładności figur płaskich, złożonych z prostych (składowych) figur geometrycznych. W tym wypadku moment bezwładności danej figury płaskiej jest równy sumie momentów bezwładności figur składowych.![]()
(2.22)
to ponieważ
r2 = z2 + y2 otrzymamy:![]()
(2.23)
W tabeli 2.2 przedstawiono wybrane momenty bezwładności i wskaźniki wytrzymałości na zginanie i skręcanie figur płaskich.
| Przekrój | Izc | Wz |
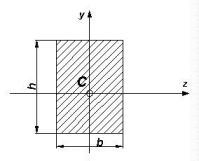 |
bh3/12 | bh2/6 |
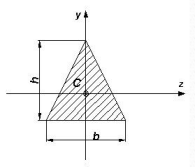 |
bh3/36 | bh2/24 |
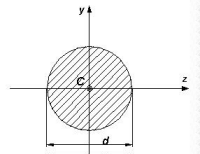 |
pd4/64 | pd3/32 |
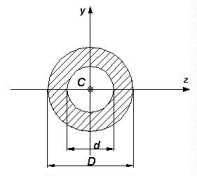 |
p(D4-d4)/64 | p(D4-d4)/32D |
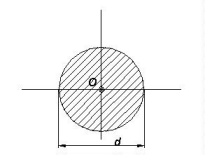 |
I0 = pd4/32 | W0 = pd3/16 |
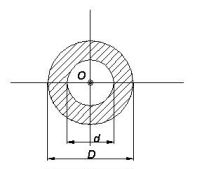 |
I0 = p(D4-d4)/32 | W0 = p(D4-d4)/16D |
Tab.2.2 Momenty bezwładności i wskaźniki wytrzymałości niektórych figór.
Pełniejszą listę wzorów i wartości momentów bezwładności oraz wskaźników wytrzymałości można znaleźć w [3].
2.3.3.4. Analiza odkształceń i naprężeń przy zginaniu, (rys.2.19)
Weźmy pod uwagę belkę o przekroju prostokątnym (b x h) poddaną czystemu zginaniu, (rys.2.19).
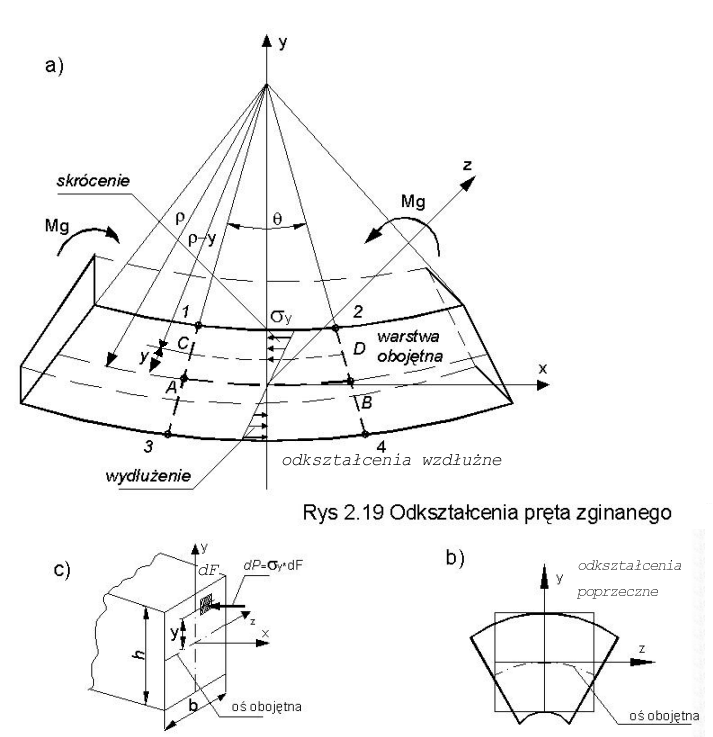
Doświadczenia przeprowadzone ze zginanymi prętami pokazują, że:
- włókna górne uległy skróceniu (rys. 2.19a) w przekroju wzdłużnym, zaś w tej części w przekroju poprzecznym pręt poszerzy się (rys. 2.19b),
- włókna dolne uległy wydłużeniu i odpowiednio zwężeniu,
- względne odkształcenia poprzeczne pręta w każdym punkcie są proporcjonalne (poprzez liczbę Poissona n ) do odkształceń wzdłużnych a więc istnieje związek między odkształceniami podobnie jak przy rozciąganiu lub ściskaniu,
- włókna równoległe do osi pręta znajdują się w jednokierunkowym stanie naprężeń (rozciąganie lub ściskanie) i nie wywierają na siebie żadnych nacisków poprzecznych,
- w strefie środkowej (warstwa obojętna) odkształcenia i naprężenia są równe zeru.
Rozważmy odkształcenia (rys. 2.19a) odcinków CD i AB. Odcinek (włókno) CD położone w odległości y od warstwy obojętnej przed odkształceniem miał długość równą AB = q r , zaś po odkształceniu CD = q
(r -y).![]()
Zaś naprężenie (zgodnie z prawem Hooke'a dla rozciągania, ściskania)
![]()
czyli rozkład naprężeń normalnych jest proporcjonalny do odległości od warstwy (osi) obojętnej (rys. 2.19a).
Weźmy pod uwagę wszystkie elementarne momenty w przekroju poprzecznym pręta (rys. 2.19c), które muszą zostać zrównoważone przez przyłożony do pręta moment zginający Mg:
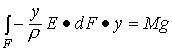
gdzie: ![]()
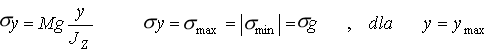
(2.24)
Wprowadzając pojęcie wskaźnika wytrzymałości przekroju na zginanie W
z jako iloraz momentu bezwładności Jz względem osi obojętnej z przez odległość ymax najdalszego włóna od tej osi, otrzymamy warunek wytrzymałościowy na zginanie: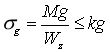
(2.25)
Dla belek zginanych wpływ naprężeń tnących od sił poprzecznych można pominąć, gdyż jest on istotny tylko przy bardzo krótkich belkach
(gdy l Ł 5h). Przypadek zginania z udziałem sił poprzecznych dla belek krótkich należy do zagadnień wytrzymałości złożonej.
2.3.3.5. Obliczenia wytrzymałościowe. Przykłady.
Przykład 2.25.
Belka dwupodporowa o długości l= 1,5m, obciążona siłą ciągłą q=5 kN / m , ma przekrój prostokątny h = 2b. Obliczyć wymiary belki, jeżeli kg = 100 MPa.
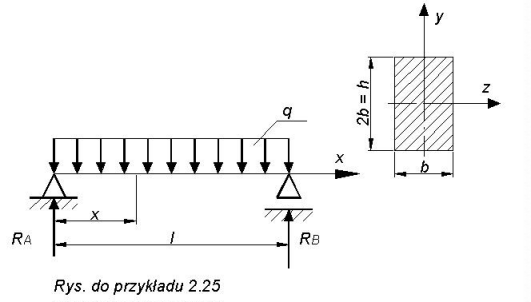
Wyznaczamy równanie momentów:
![]()
gdzie reakcje Ra i Rb wyznaczamy z warunków równowagi:
![]()
Znajdujemy max, moment gnący dla

Korzystając ze wzoru (2.25) oraz (tab. 2.2) ze wzoru na wskaźnik W
zOtrzymamy:
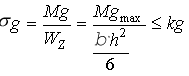
Stąd wymiary belki:
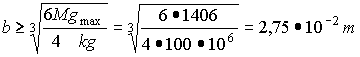
hł 5,5 * 10-2 m
Bardzo często zachodzi potrzeba zaprojektowania belki o równej wytrzymałości. Jest to belka, w której w każdym jej przekroju naprężenia maksymalne są równe naprężeniom dopuszczalnym.
Przykład 2.26.
Z
aprojektować belkę wspornikową o równej wytrzymałości, o przekroju prostokątnym o stałej szerokości b.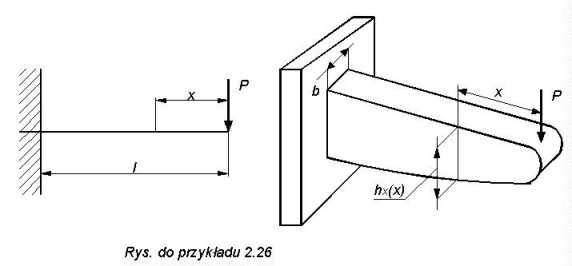
Korzystając z wzoru (2.25) warunek równej wytrzymałości ma postać sg = kg w każdym przekroju belki.
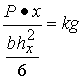
Ponieważ belka ma stałą szerokość, więc wysokość h
x będzie zależeć od miejsca położenia przekroju x.
Wysokość belki będzie zmieniać się paraboliczne od x=O do x=l. Wykonanie belek o takim kształcie jest kłopotliwe i kosztowne, przeto przyjmuje się uproszczony kształt opisany na profilu teoretycznym. Przykładem belki stopniowanej będzie między . innymi resor, wałek ze stopniowanymi średnicami.
Przykład 2.27.
Płaska sprężyna stykowa wykonana z materiału o własnościach E=1,2ˇ10
5 MPa, kg = 60 MPa i wymiarach przekroju poprzecznego b = 1O h, obciążona jak na rysunku P = 0,1 N.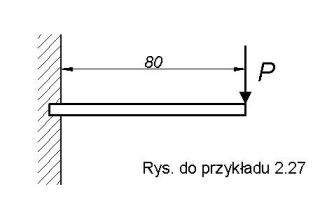
Odp. Wymiary tej sprężyny wynoszą : b=5 mm , h=0,5 mm
Przykład 2.28.
Obliczyć średnicę stalowej belki (kg=120 MPa) obciążonej jak n
a rysunku.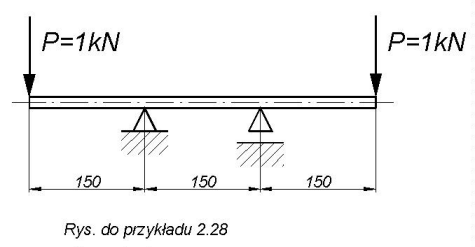
Odp. Średnica belki wynosi d=3,625 10
-2 m.