Wytrzymałość prosta

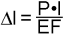
2.3. Wytrzymałość prosta

2.3.1. Rozciąganie i ściskanie

2.3.1.1. Zachowanie się materiałów w zakresie odkształceń sprężystych

Zachowanie się sprężyste ciała stałego w całości jest sumarycznym skutkiem indywidualnych odkształceń jego wiązań, podczas gdy siła przyłożona w jednym punkcie ciała przenosi się wzdłuż sieci wiązań, biegnących przez materiał do drugiego punktu ciała, w którym jest przyłożona druga siła równoważąca pierwszą.

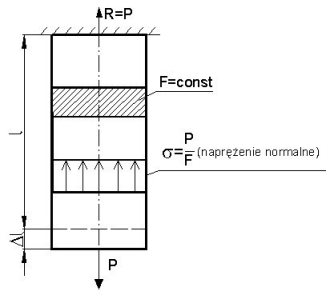
Rys. 2.8 Ilustracja do prawa Hooke'a

Gdy siły przyłożone są dostatecznie małe, przemieszczenie sprężyste jest zawsze proporcjonalne do siły:

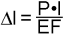
(2.3)

Przyjmując wydłużenie względne:

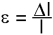
(2.4)

oraz naprężenie rozciągające:

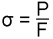
(2.5)

Prawo Hooke'a przy rozciąganiu (jak i ściskaniu), ma postać:

s = e * E

(2.6)

Współczynnik proporcjonalności E nosi nazwę modułu sprężystości wzdłużnej (modułu Younga). Dla stali (w temp. + 20^oC) moduł ten wynosi:

E = 2,1*10⁵MPa @ 2,1*10⁶kG/cm²

Wartości modułów Younga dla różnych materiałów podano w literaturze [1] [3] [4]
Proporcjonalność naprężenia do odkształcenia zachowana jest tylko przy niewielkich wydłużeniach względnych.

Jeśli materiał ciągliwy, będziemy rozciągać ponad określone naprężenie (np. granicę sprężystości czy też granicę plastyczności) to zacznie się on odkształcać plastycznie. Odkształcenia sprężyste są zwykle nieznaczne (i nadal podlegają prawu Hooke'a) zaś odkształcenia plastyczne znacznie je przewyższają.

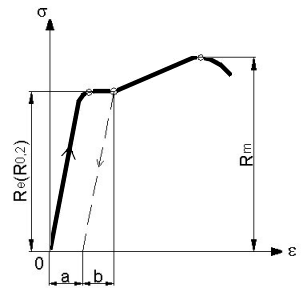
Rys. 2.9 Krzywa rozciągania: a - odkształcenie trwałe, b - odkształcenie sprężyste

Jeżeli próbkę odciążymy, to odkształcenie sprężyste znika z takim samym współczynnikiem proporcjonalności E, zaś odkształcenie plastyczne pozostaje jako odkształcenie trwałe.

2.3.1.2. Naprężenia dopuszczalne. Zasada superpozycji.

Obciążenia mechaniczne, termiczne danego elementu maszynowego mogą doprowadzić do zmiany stanu naprężeń uniemożliwiającej dalsze jego eksploatowanie. Jak widać z rys. 2.9, naprężenia mogą osiągać wartość graniczną (Rm) i próbka ulegnie zerwaniu. Równie niekorzystnym może być powstanie odkształceń plastycznych (R_e, R_0,2) trwałych.
W celu zabezpieczenia się przed taką sytuacją należy określić graniczną wartość naprężenia nieprzekraczalną w danych warunkach pracy elementu. Tę wartość naprężenia nazywamy naprężeniem dopuszczalnym na rozciąganie (k_r).
W obliczeniach wytrzymałościowych musi więc być spełniony warunek:

s Ł k_r gdzie:

;

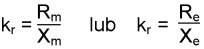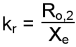
(2.7)

Współczynniki (X_m, X_e) nazywamy współczynnikami bezpieczeństwa w odniesieniu do wytrzymałości na rozciąganie (R_m) oraz w odniesieniu do granicy plastyczności (R_e, R_o,2).
Przy ustalaniu wartości współczynnika bezpieczeństwa należy uwzględnić warunki pracy, rodzaj materiału, ,rodzaj obciążeń, niedokładność obliczeń wytrzymałościowych, wielkość elementu.
W tabeli 2.1. przedstawiono przeciętne wartości współczynników bezpieczeństwa, którymi można, się posługiwać przy obliczeniach wytrzymałościowych.

	Współczynniki bezpieczeństwa	Współczynniki bezpieczeństwa
Materiał	X_e	X_m
stale staliwo żeliwo ciągliwe	2 - 2,3	-
żeliwo szare	-	3,5
mosiądze	3	-
brązy	3,5	-
stopy aluminium	3,9	-
stopy magnezu	3,9	-

Tab. 2.1 Przeciętne wartości współczynników bezpieczeństwa wg [2]

W wielu dziedzinach budowy maszyn (zbiorniki ciśnieniowe, konstrukcje stalowe) obowiązują odrębne przepisy państwowe zobowiązujące do przestrzegania odpowiednich współczynników bezpieczeństwa.
Przy rozwiązywaniu zagadnień wytrzymałościowych często można skorzystać z zasady superpozycji, która pozwala znacznie uprościć obliczenia.
Załóżmy, że ciało sprężyste ulega wydłużeniu Dl₁ pod działaniem siły P₁ oraz wydłużenia Dl₂ pod wpływem siły P₂. Jeżeli wydłużenia Dl₁ i Dl₂ są małe (naprężenia nie przekraczają granicy proporcjonalności s_prop ) oraz liniowe (podlegają prawu Hooke'a), to równoczesny wpływ P₁ i P₂ na ciało powoduje jego wydłużenie o Dl₁+Dl₂ . Zasady superpozycji nie wolno stosować w tych przypadkach, gdy działanie jednych sił zmienia charakter działania innych sił .

2.3.1.3. Układy statycznie wyznaczalne. Przykłady.

Przykład 2.7.

Obliczyć wydłużenie Dl pręta obciążonego siłami P₁,P₂,P₃.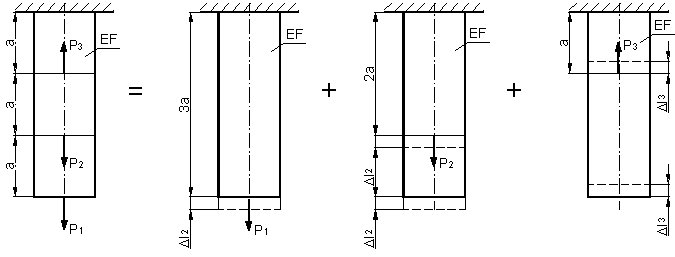

Rys. do przykł. 2.7

Posługując się metodą superpozycji wyznaczymy wydłużenie l pręta obciążonego siłami P₁,P₂,P₃.Stan wyjściowy będzie sumą trzech stanów prostych.
Gdyby pręt był obciążony tylko siłą P₁:

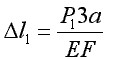
Gdyby pręt był obciążony tylko siłą P₂: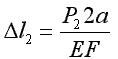

Gdyby pręt był obciążony tylko siłą P₃: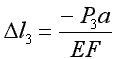

Całkowite wydłużenie jest sumą wydłużeń obliczonych dla poszczególnych stanów prostych:

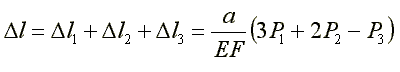
Przykład 2.8.

Sporządzić wykres sił i naprężeń normalnych dla pręta pokazanego na rysunku. Obliczyć całkowite wydłużenie pręta.

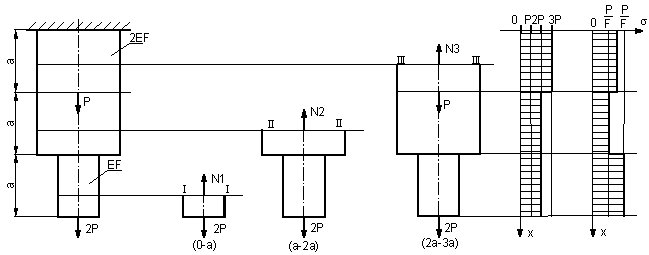
Rys. do przykładu 2.8.a

a) metoda przecięć:

Rozważmy przekrój I-I

N₁-2P=0 N₁=2P

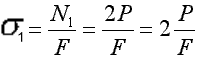
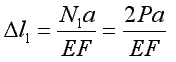
Rozważmy przekrój II-II

N₂-2P=0 ; N₂=2P

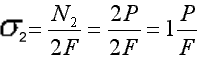
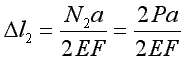
Rozważmy przekrój III-III

N₃-2P-P=0 N₃=3P

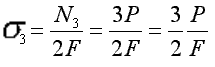
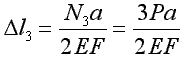
Wydłużenie całkowite pręta:

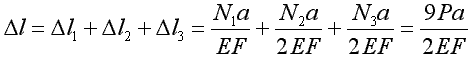
b) metoda superpozycji:

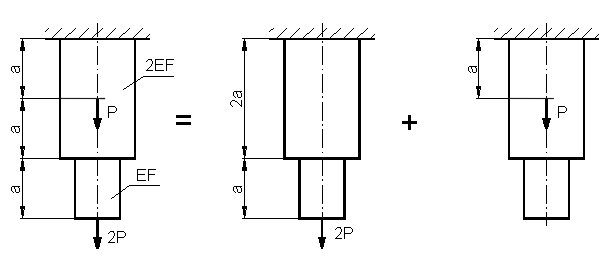
Rys. do przykł. 2.8.b

Gdyby pręt był obciążony tylko siłą 2P:

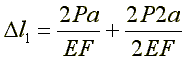
Gdyby pręt był obciążony tylko siłą P:

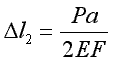
Wydłużenie całkowite pręta:

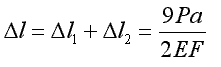
Przykład 2.9.

Układ prętowy przedstawiony na rysunku obciążony jest siłą P = 400 N.
Długość pręta wynosi l = 800 mm a średnica d = 3 mm. Moduł Younga materiału pręta E = 100 kN/mm² . Obliczyć naprężenia w prętach oraz przemieszczenie pionowe punktu C.

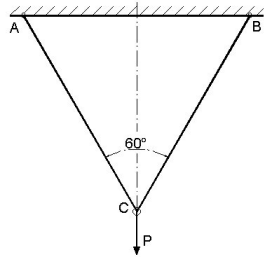
Rys. do przykł. 2.9.

Z warunku równowagi węzła C znajdujemy:

2S cos 30^o - P = 0 ; S = 231 N

Naprężenia w prętach wynoszą:

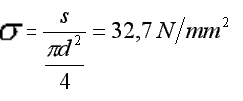
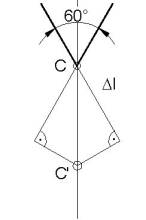
Oba pręty wydłużą się o l oraz obrócą wokół punktów zamocowania (A i B).
Dla niewielkich odkształceń łuk okręgu można zastąpić styczną.

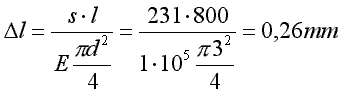
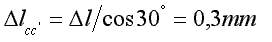
Przykład 2.10

Sporządzić wykres sił i naprężeń normalnych dla pręta pokazanego na rysunku. Obliczyć całkowite wydłużenie pręta.

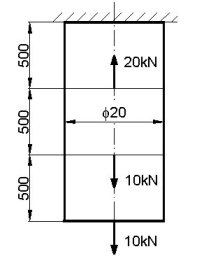
Rys. do przykł. 2.10.

Odp.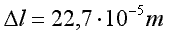

Przykład 2.11.

Obliczyć i wykonać wykres naprężeń normalnych we wszystkich częściach pręta stalowego, pokazanego na rysunku. Obliczyć całkowite wydłużenie pręta.

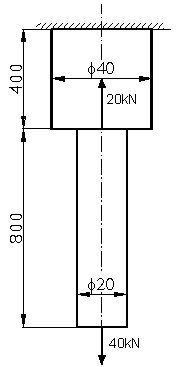
Rys. do przykł. 2.11.

Odp.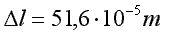

Przykład 2.12.

Na wysięgniku złożonym ze stalowej podpory AC i stalowego pręta BC powieszono ciężar Q=50 kN . Obliczyć średnicę podpory AC i pręta BC .

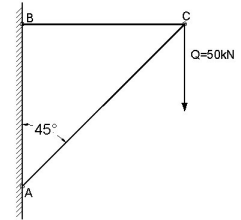
Rys. do przykł. 2.12

Odp. Średnica podpory AC wynosi 24 , a średnica pręta BC 20 .

2.3.1.4. Układy stycznie niewyznaczalne. Przykłady.

Układy takie są nierozwiązywalne na gruncie statyki ciał doskonale sztywnych (por. Rozdz. 2.2.). Rozwiązanie takich układów można uzyskać dopiero, gdy uwzględni się odkształcenia ciał wchodzących w skład danego układu.

Przykład 2.13.

Obliczyć reakcje utwierdzenia pręta między sztywnymi i nieprzesuwnymi ścianami.

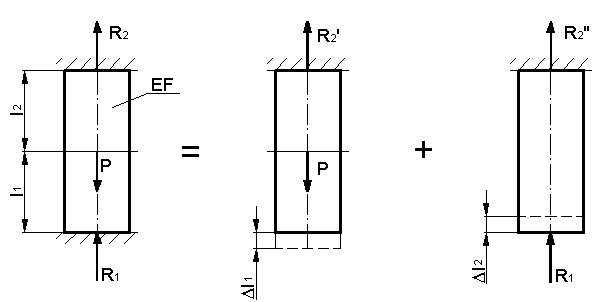
Rys. do przykł. 2.13.

Oznaczamy reakcje utwierdzenia R₁,R_{2 ,}z warunku równowagi mamy :

R₂-P+R₁=0

Brakujące równanie otrzymamy z porównania odkształceń: l₁-l₂=0
Posługując się metodą superpozycji wyznaczymy wydłużenia l₁, l₂.

;

otrzymamy:

;

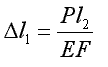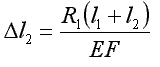
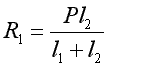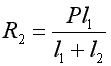
Istotne znaczenie w układach statycznie niewyznaczalnych mają naprężenia własne (wstępne) powstające w nie obciążonym jeszcze układzie.
Powstają one na skutek niewłaściwego wykonania i montażu niektórych elementów układu. Jeżeli układ obciążymy siłami zewnętrznymi, to naprężenia wywołane tymi siłami współdziałają z naprężeniami własnymi, powodując zmianę stanu naprężeń w tym układzie.

Przykład 2.14.

Nieodkształcalna belka ma być zawieszona na czterech jednakowych prętach o sztywności EF. W czasie montażu stwierdzono, że dwa pręty środkowe są krótsze od prętów skrajnych o wielkość e.
Jakie siły wystąpią we wszystkich prętach z chwilą likwidacji szczeliny e?

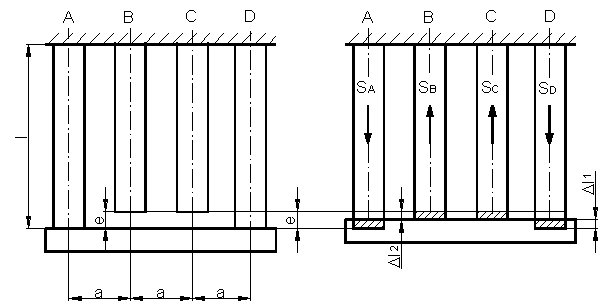
Rys. do przykł. 2.14.

Przy montażu pręty skrajne A i D uległy skróceniu o l₁, zaś pręty środkowe B i C wydłużeniu o l₂.

Ze względu na symetrię układu:

S_A = S_D = S₁S_B = S_C = S₂

Z warunku równowagi układu:

-S_A + S_B + S_C - S_D = 0
Z (1) i (2) otrzymamy S₁ = S₂

Z warunku odkształceń (przy założeniu, że e << l):

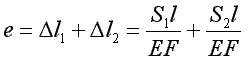
Z powyższych równań otrzymamy:

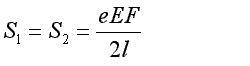
W układach statycznie niewyznaczalnych zmiany temperatury wywołują dodatkowe naprężenia zwane termicznymi (np. szyny tramwajowe) .

Przykład 2.15.

Obliczyć, jakie naprężenia powstaną w pręcie zamocowanym między dwiema sztywnymi nieprzesuwnymi ścianami po ogrzaniu go o t.

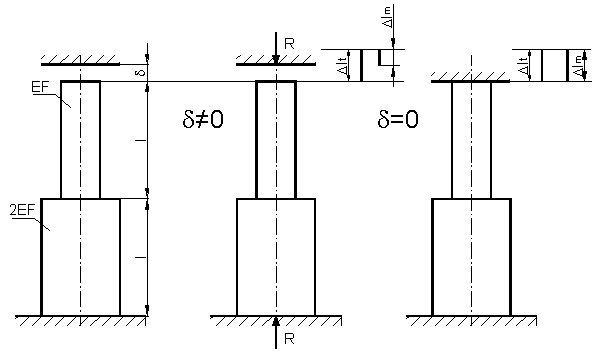
Rys. do przykł. 2.15.

Luz d ≠ 0 zniknie przy wzroście temperatury o ∆t₀:

∆l₀ = d = a 2l ∆t₀

Dla ∆t>∆t₀ w ścianach wystąpią reakcje R. Pręty wydłużyły się pod wpływem przyrostu ∆t temperatury o ∆l_t oraz ulegnie skróceniu pod wpływem reakcji R o ∆l_m.
Z warunku odkształceń przy założeniu d << l otrzymamy:

∆l_t= ∆l_m+ d
∆l_t= a 2l ∆t

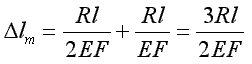
Po obliczeniach otrzymamy:

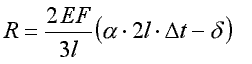
Naprężenia w części (2EF):

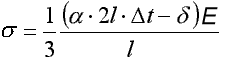
Naprężenia w części (EF):

Gdy luz d = 0, z warunku odkształceń otrzymamy:

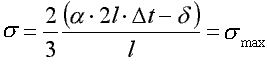
∆l_t = ∆l_m i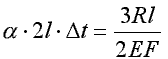

Największe naprężenia wystąpią w części (EF):

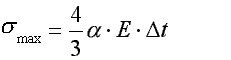
Przykład 2.16.

Wyznaczyć siły w prętach układu obciążonego siłą W przedstawionego na rysunku. Sztywność prętów wynosi EF.

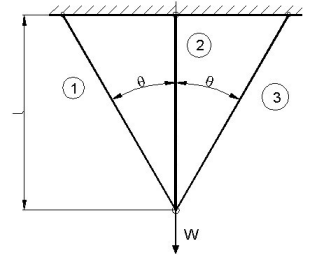
Rys. do przykł. 2.16.

Odp.

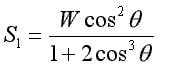, napięcie w skrajnych prętach

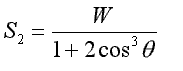, napięcie w środkowym pręcie

Przykład 2.17.

Wyznaczyć siły w prętach, na których zawieszono sztywną belkę (ciężar jej pomijamy), przegubowo w punkcie A. Belkę obciążono siłą P.

Odp. ,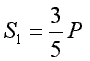

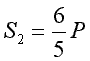
Przykład 2.18.

Obliczyć reakcje ścian (utwierdzenia) po podgrzaniu stalowego pręta o ∆t.

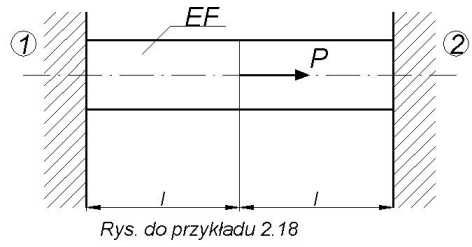
Odp. ,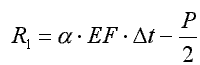

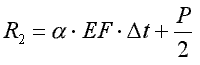
2.3.1.5 Związki między naprężeniami a odkształceniami w stanie sprężystym

A. Naprężenia w jednokierunkowym stanie napięcia

Weźmy pod uwagę pręt o przekroju F = const. I zbadajmy stan napięcia w dowolnym punkcie A (rys 2.10).
Rozłóżmy naprężenie p_ana dwa wzajemnie prostopadłe kierunki (n , ).

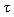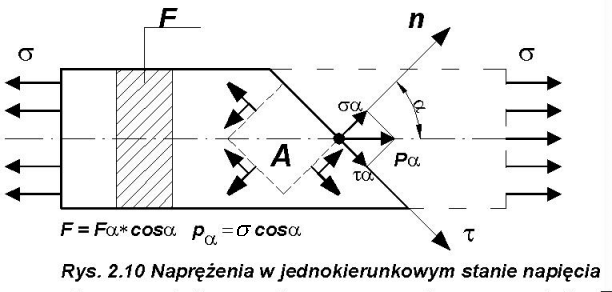
otrzymamy:

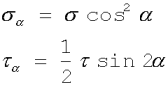
(2.8)

Wytnijmy z rozpatrywanego pręta element prostopadłościenny zawierający punkt A. Wyznaczmy teraz naprężenia normalne s i styczne t na kolejnych ściankach (90°+ a , 180°+ a , 270°+ a ), a otrzymamy:

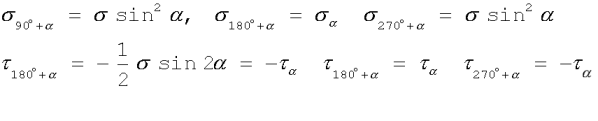(2.9)

Z otrzymanych wzorów wynikają wnioski:

1. Naprężenia s i t występujące na dwóch równoległych do siebie przekrojach są odpowiednio równe: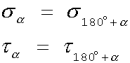

2. Na dwóch wzajemnie prostopadłych ścianach naprężenia t są równe co do bezwzględnej wartości: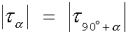

B. Naprężenia w dwukierunkowym stanie napięcia:

Weźmy pod uwagę płaską blachę o przekroju F = const i zbadajmy stan napięcia w dowolnym punkcie A (rys. 2.11).

Podobnie jak w pkt. a otrzymamy:

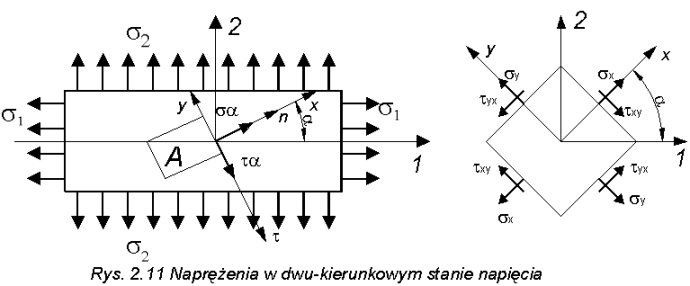
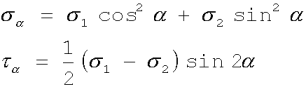
(2.10)

Ze wzoru (2.10) widać, że istnieją przekroje (a = 0, a = p /2), w których naprężenia styczne wynoszą zero.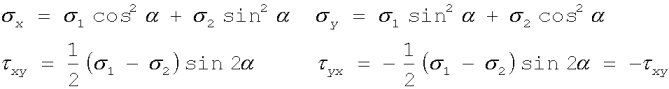
Takie przekroje, w których t _a = 0, a działają jedynie naprężenia normalne s _a , nazywamy przekrojami głównymi, naprężenia normalne w tych przekrojach - naprężeniami głównymi, a kierunki działania tych naprężeń - kierunkami głównymi.
Wytnijmy z rozpatrywanej blachy element prostopadłościenny zawierający punkt A. Oznaczmy współrzędne x, y, otrzymamy podobne wzory i wnioski jak w pkt. a.

(2.11)

Aby określić naprężenia w płaskim stanie napięcia wystarczy znać wartości naprężeń normalnych występujących na dwóch wzajemnie prostopadłych przekrojach oraz naprężenie styczne w jednym z tych przekrojów.
Z kolei znając s _x, s _y oraz t możemy określić naprężenia główne ze wzorów:

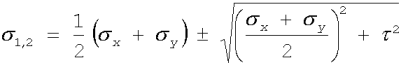
(2.12)

oraz kierunek główny, jaki tworzy s ₁ z s _x: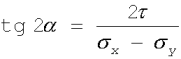

(2.13)

Ze wzoru (2.10) wynika, że największe naprężenie (tnące) t _maxwystępuje w przekrojach tworzących kąty 45° z kierunkami głównymi.

C. Zmiana wymiarów poprzecznych rozciąganego pręta

Podczas próby rozciągnięcia pręt wydłuży się o D l zgodnie ze wzorem (2.3). Jednocześnie, w miarę jak pręt się wydłuża, jego wymiary poprzeczne zmniejszają się. Pod działaniem naprężeń rozciągających s pręt wydłuży się o wartość e = s /E wg wzoru (2.6). Jeżeli s nie przekroczy s _prop, to wymiary poprzeczne pręta ulegną zmniejszeniu o wartość n * e . Występujący tutaj współczynnik proporcjonalności n nazywany jest liczbą Poissona. Można udowodnić, że współczynnik ten jest nie większy niż: n Ł 1/2. Wartość liczby Poissona n dla niektórych materiałów podano [3],[4].

D. Prawo Hooke'a w płaskim i przestrzennym stanie napięcia

Jeżeli elementarną kostkę sześcienną poddamy działaniu naprężeń s₁, s₂, s₃ i wyznaczymy odpowiadające im odkształcenia względne e₁, e₂, e₃, to stosując zasadę superpozycji otrzymamy wzory na związki naprężeń z odkształceniami w przestrzennym stanie sprężystym: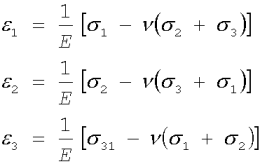

(2.14)

Wzory na związki w płaskim stanie napięcia otrzymamy z wzorów (2.14) po opuszczeniu w każdym wierszu naprężenia s ₃. Wzory powyższe są słuszne, gdy żadne z naprężeń nie przekracza granicy proporcjonalności s _prop.